radial basis functions

_{scroll ↓ to Resources}

Note

any basis function are used to transform dataset features and amend the design matrix
other (non-radial) basis functions examples: polynomial, Fourier, etc.
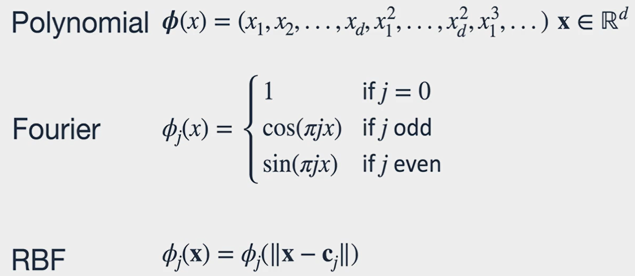
the locality principle - the general idea of shallow ML is that training set elements located nearby and having relatively short distance between each other should have the same label and belong to the same class. Deep learning is not based on this principle, because of the huge dimentionality of input vectors.
each RBF creates a new feature, which value is dependent on the distance between each sample and some center point
==RBF facilitates non-linearity== in predictive models

reminds the normal distribution probability density function
when $x_{i} == c_{j}$ ⇒ $φ_{j} == 1$
- the more closer x is to the chosen center, the closer the RBF value is to 1
- when distance is growing φ goes to 0
- it doesn’t have the notion of direction, the distance is scalar and all points on a circle are seen similarly for one RBF, that’s why we need more of them
RBF centers are usually picked up randomly and uniformly from training set samples ensuring that clusters with more data points get more RBF centers around

as in the picture above with 3 RBF centers, RBF breaks linearity of the model
- same feature vector change by $Δ x$ for two samples $x 1 - > x 1 + Δ x$ and $x 2 - > x 2 + Δ x$ will not lead to the same target prediction change, given that the data points have different distances to the chosen centers
hyperparameters are the number of centers and the width (or bandwidth)
- the optimal number of centers is dependent on data locality: the more clusters there are in the data, the more center points are needed
- generally speaking, the more centers, the less bandwidth, because ==all the Gaussians collectively need to cover complete feature space==

table file.inlinks, file.outlinks from [[]] and !outgoing([[]])  AND -"Changelog"