logistic regression
scroll ↓ to Resources
Contents
- Note
- Intuition and connection to linear regression
- Derivation of the cross-entropy loss function
- Cross-entropy minimization
- Resources
Note
- Logistic regression is a linear model that solves a classification problem using the softmax function, which outputs discrete probability values for each class (not a class label itself)
- In such view, even the modern neural networks can be seen as sophisticated algorithms generating advanced characteristics to which logistic regression is then applied as one of the last layers.
- Being a linear model, it allows interpretability
- weights matrix W of the model reveals which characteristics of input are decisive for each class attribution
Intuition and connection to linear regression
- One can see the task of classification into K classes as K linear regression Z_i to Z_k where each one is predicting the probability of belonging to the i-th class.
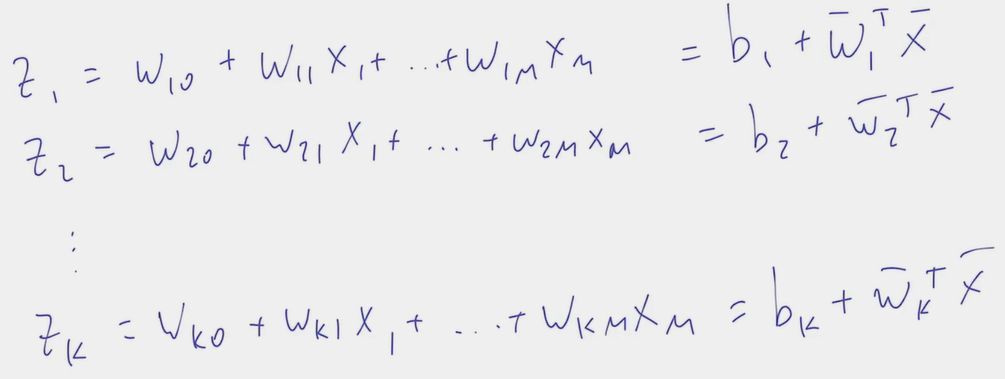
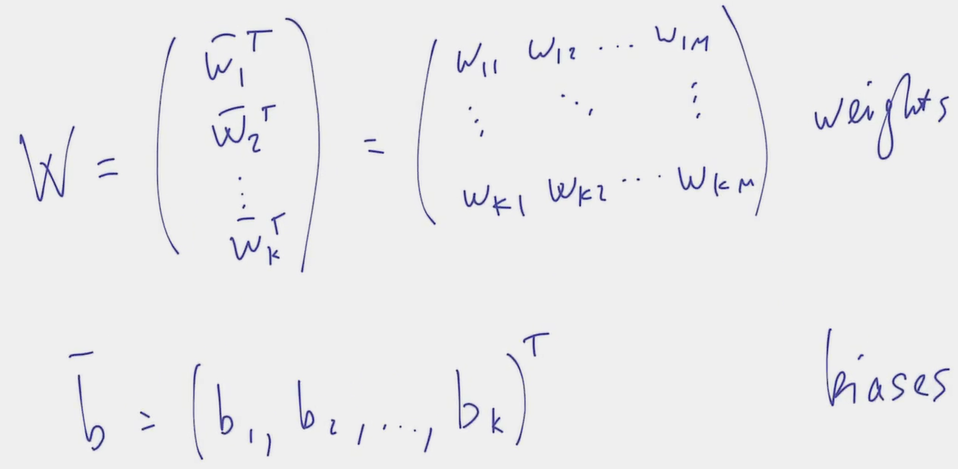
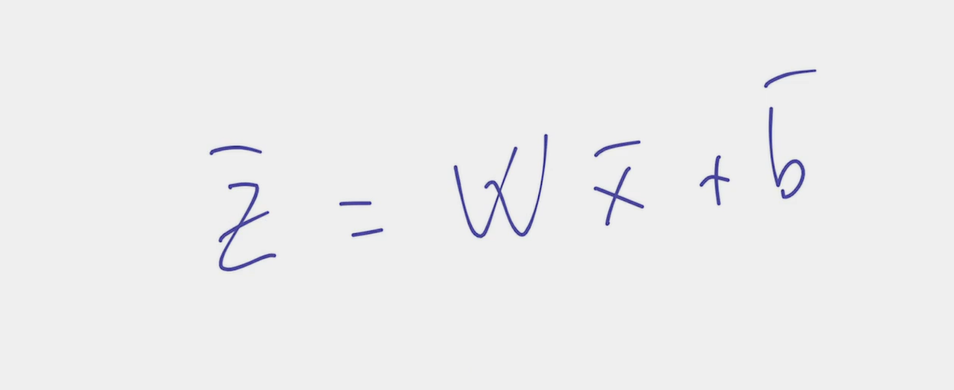
- The challenge is two-fold:
- how to make regression predict the probability?
- if the selected loss function (see derivation below) is boolean-output (specific class label), its partial derivatives will be 0 as the output class is not changing when the input vectors are changed by infinitely small values (like gradient descent would need). Therefore, we don’t want it to output classes directly.
- if we can find a wrapping function such that is a confidence\probability value which is the input of the loss function
- the 1st issue is solved by design
- The loss function is now dependent not on the class itself, but on the probability of that class, which in turn can change due to infinitely small change in input values. ⇒ Partial derivatives are not 0.
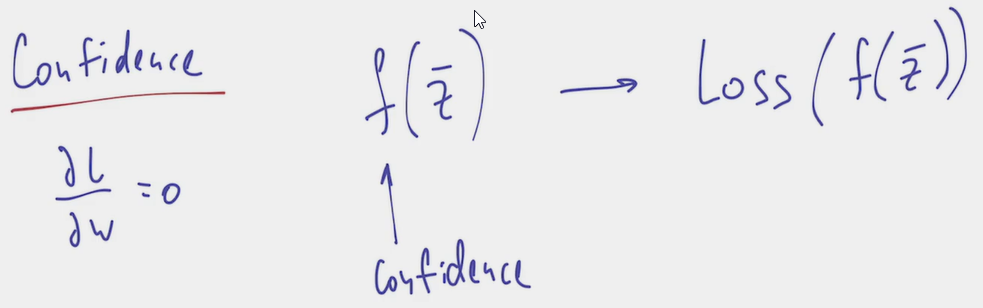
- Which characteristic should the function f possess to satisfy our needs?
- all components are non-negative
- all components are summed to 1
- if then
- Partial derivatives of any component by any of the learnable parameters not equal to 0:
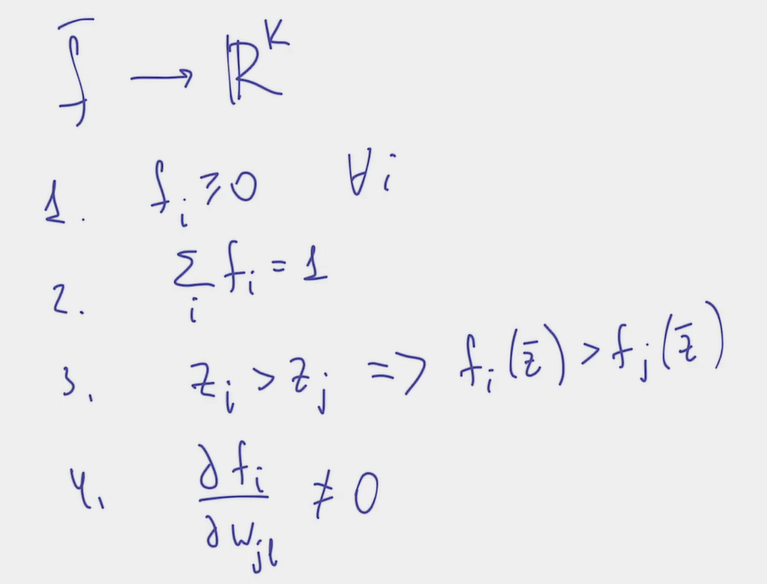
- Such a function satisfying all requirements exists and it’s called softmax
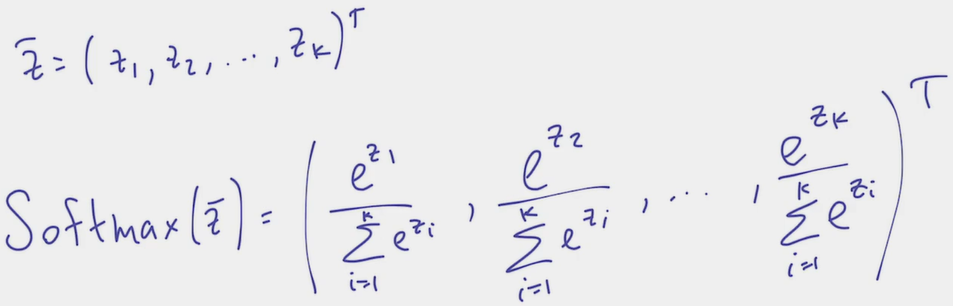
- As a result, the logistic regression algorithm is nothing else than , where is our set of trainable parameters
- states the algorithm’s opinion about the probability that the object described by belongs to class
Derivation of the cross-entropy loss function
- Our algorithm is
- Referring to the maximum likelihood principle, we want that the reality we actually observe is perceived as highly likely by our algorithm and something we don’t observe in reality also has low probability according to the algorithm
- Ideally, we want to train the algorithm in such a way that for each in our dataset there is a corresponding class label .
- For one particular the probability of this happening is
- For this to happen for all dataset objects (assuming all objects are independently sampled) this is a joint probability
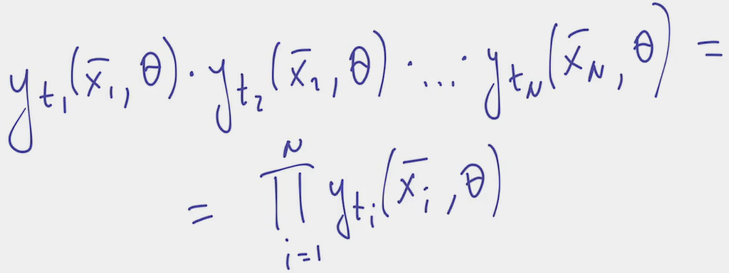
- This joint probability we want to maximize. We can already take -log() of the expression and minimize it, but, conventionally, some further modifications are made to come to the cross-entropy function.
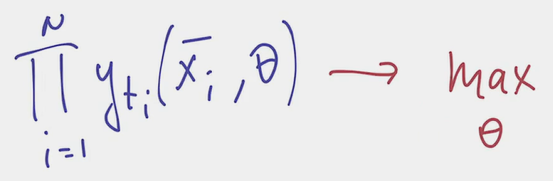
- The modification uses the insight that class label is essentially a vector consisting of a single 1 and the rest 0 ([one hot encoding])
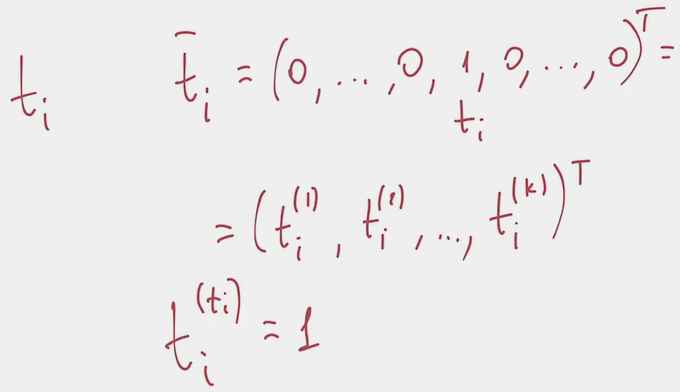
- With this vector in place, the previous can be rewritten: Iterating over all components of the one hot encoded vector, we multiply all softmax outputs to the power of the corresponding component of one hot encoding vector.
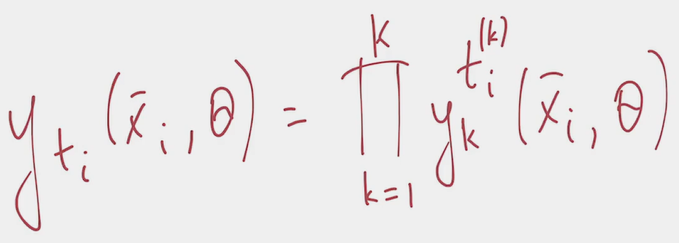
- All one hot encoding components but one are 0. Anything to the power of 0 is 1, therefore in the multiplication above all but one components are 1. That only non-1 component corresponds to the correct class yielding:
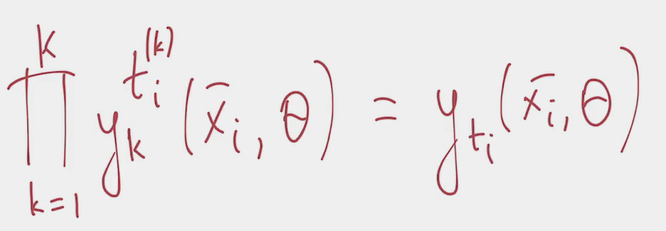
- this formulation for can be fed back into the max likelihood formula above:
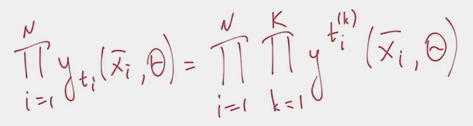
- Further, for easier optimization, summation is preferred to multiplication, so we take a of that with the minus sign (to make it a minimization task for traditions sake).
- In the result we derived the cross-entropy loss function suitable for classification tasks:
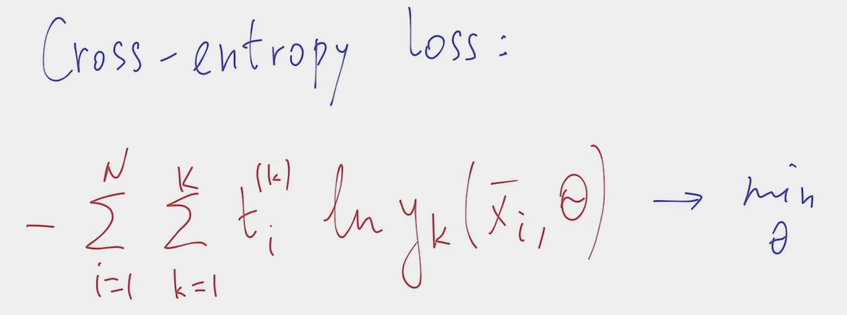
- class disbalance has negative effect, because the cross-entropy formula contains iteration over every training sample from 1 to N. Overrepresented class will have a larger impact on the loss function value and the algorithm will prioritize correct classification of that one
Cross-entropy minimization
- Unlike for linear regression where it was possible to solve the system of equations directly, here it’s not possible to do without the iterative gradient descent.
- don’t forget data normalization to the range from -1 to 1
Resources
Links to this File
table file.inlinks, file.outlinks from [[]] and !outgoing([[]]) AND -"Changelog"